A class providing affine transformations. More...

#include <egs_transformations.h>

Public Member Functions
	EGS_AffineTransform ()
	Constructs a unit affine transformation.

	EGS_AffineTransform (const EGS_AffineTransform &tr)
	Copy constructor.

	EGS_AffineTransform (const EGS_RotationMatrix &m, const EGS_Vector &v)
	Constructs an affine transformation object from the rotation m and translation v.

	EGS_AffineTransform (const EGS_RotationMatrix &m)
	Constructs an affine transformation object from the rotation m, which has no translation.

	EGS_AffineTransform (const EGS_Vector &v)
	Constructs an affine transformation object from the translation v, which has no rotation.

EGS_AffineTransform	operator* (const EGS_AffineTransform &tr) const
	Returns the multiplication of the invoking object with tr. More...

EGS_AffineTransform	operator* (const EGS_RotationMatrix &m) const
	Returns the affine transformation $(R \cdot m, \vec{t})$ , where and $\vec{t}$ are the rotation and translation of the invoking object.

EGS_AffineTransform &	operator*= (const EGS_AffineTransform &tr)
	Multiplies the invoking object from the right with tr. Returns a reference to the result. More...

EGS_AffineTransform &	operator*= (const EGS_RotationMatrix &m)
	Multiplies the invoking object from the right with m. Returns a reference to the result. More...

EGS_AffineTransform	operator+ (const EGS_Vector &v) const

EGS_AffineTransform &	operator+= (const EGS_Vector &v)

EGS_Vector	operator* (const EGS_Vector &v) const
	Applies the transformation to the vector v from the left and returns the result.

void	transform (EGS_Vector &v) const
	Transforms the vector v.

void	inverseTransform (EGS_Vector &v) const
	Applies the inverse transformation to the vector v.

EGS_AffineTransform	inverse () const
	Returns the inverse affine transformation.

void	rotate (EGS_Vector &v) const
	Applies the rotation to the vector v.

void	rotateInverse (EGS_Vector &v) const
	Applies the inverse rotation to the vector v.

void	translate (EGS_Vector &v) const
	Applies the translation to the vector v.

const EGS_Vector &	getTranslation () const
	Returns the translation vector of the affine transformation object.

const EGS_RotationMatrix &	getRotation () const
	Returns the rotation matrix of the affine transformation object.

bool	isI () const
	Returns `true` if the object is a unity transformation, `false` otherwise.

bool	hasTranslation () const
	Returns `true` if the transformation involves a translation, `false` otherwise.

bool	hasRotation () const
	Returns `true` if the transformation involves a rotation, `false` otherwise.

Static Public Member Functions
static EGS_AffineTransform *	getTransformation (EGS_Input *inp)
	Constructs an affine transformation object from the input pointed to by inp and returns a pointer to it. More...

Protected Attributes
EGS_RotationMatrix	R

EGS_Vector	t

bool	has_t

bool	has_R

Friends
EGS_Vector	operator* (const EGS_Vector &v, const EGS_AffineTransform &tr)
	Applies the transformation tr to the invoking vector from the right and returns the result.

EGS_Vector &	operator*= (EGS_Vector &v, const EGS_AffineTransform &tr)
	Applies the transformation tr to the invoking vector from the right, assignes the result to v and returns a reference to it.

Detailed Description

A class providing affine transformations.

An affine transformation $T = (R,\vec{t})$ consists of a rotation $R$ and a translation $\vec{t}$ , so that $T \vec{x} = R \vec{x} + \vec{t}$ . See the getTransformation() documentation for description of the keys needed to define an affine transformation.

Examples:: geometry/egs_box/egs_box.cpp.

Definition at line 417 of file egs_transformations.h.

Member Function Documentation

EGS_AffineTransform EGS_AffineTransform::operator* ( const EGS_AffineTransform & tr ) const

Returns the multiplication of the invoking object with tr.

The multiplication of 2 affine transformations $T_1=(R_1,\vec{t_1})$ and $T_2=(R_2,\vec{t_2})$ is defined as the affine transformation $T=(R,\vec{t})$ which, when applied on any vecor $\vec{x}$ , results in the same vector that one would obtain by first transforming it with $T_1$ and then with $T_2$ . It is easy to see that $R = R_2 \cdot R_1$ and $t = R_2 \cdot \vec{t}_1 + \vec{t}_2$ .

Definition at line 485 of file egs_transformations.h.

EGS_AffineTransform& EGS_AffineTransform::operator*= ( const EGS_AffineTransform & tr )

Multiplies the invoking object from the right with tr. Returns a reference to the result.

See Also: operator *(EGS_AffineTransform &)

Definition at line 501 of file egs_transformations.h.

EGS_AffineTransform& EGS_AffineTransform::operator*= ( const EGS_RotationMatrix & m )

Multiplies the invoking object from the right with m. Returns a reference to the result.

See Also: operator *(EGS_RotationMatrix &)

Definition at line 510 of file egs_transformations.h.

EGS_AffineTransform * EGS_AffineTransform::getTransformation ( EGS_Input * inp )

static

Constructs an affine transformation object from the input pointed to by inp and returns a pointer to it.

A transformation is defined in the input file using the following set of keys:

:start transformation:
    translation = tx, ty, tz
    rotation    = 2, 3 or 9 floating point numbers
    or
    rotation vector = 3 floating point numbers
:stop transformation:

There are many different ways to define a rotation. The rotation vector input defines a rotation which, when applied to the 3D vector defined by the input, transforms it into a vector along the positive z-axis. For instance, if one wanted to have a rotation of +45 degrees around the y-axis, one would use -1,0,1 as input to the rotation vector key. The input to the rotation key is interpreted as follows:

If followed by two floating point numbers, this input defines a rotation by the polar angle 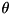$\theta$ defined by the second input and the azimuthal angle 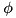$\phi$ defined by the first input with both angles considered to be in radian (i.e. a rotation by 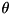$\theta$ around the x-axis followed by a rotation by 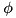$\phi$ around the z-axis)
If followed by three floating point numbers, this input defines a rotation that is the combination of a rotation by the third input in radian around the z-axis, followed by a rotation by the second input around the y-axis, followed by a rotation by the first input around the x-axis.
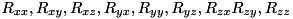If followed by 9 floating point numbers, the 9 numbers are considered as the 9 elements of a 3x3 rotation matrix in the order $R_{xx}, R_{xy}, R_{xz}, R_{yx}, R_{yy}, R_{yz}, R_{zx} R_{zy}, R_{zz}$ .

Examples:: geometry/egs_box/egs_box.cpp.

Definition at line 43 of file egs_transformations.cpp.

References EGS_AffineTransform(), egsWarning, EGS_Input::getInput(), EGS_RotationMatrix::inverse(), EGS_Input::isA(), EGS_RotationMatrix::isRotation(), EGS_RotationMatrix::rotZ(), and EGS_Input::takeInputItem().

Referenced by EGS_BoxShape::createObject(), EGS_CylinderShape::createObject(), EGS_AEnvelope::createTransforms(), EGS_TransformedSource::EGS_TransformedSource(), EGS_GeometryTester::getGeometryTester(), and EGS_BaseShape::setTransformation().

The documentation for this class was generated from the following files:

/home/rwtownson/EGSnrc/HEN_HOUSE/egs++/egs_transformations.h
/home/rwtownson/EGSnrc/HEN_HOUSE/egs++/egs_transformations.cpp

Public Member Functions

Static Public Member Functions

Protected Attributes

Friends

Detailed Description

Member Function Documentation